第三章 神经网络

根据理论, 无论怎样复杂的函数, 只要感知机足够多, 都可以表示出来. 重点在于怎么设计权重. 对于复杂的多层感知机, 权重的确定十分困难.

神经网络可以解决这个问题, 它可以从数据中学习到合适的权重.

3.1 从感知机到神经网络

3.1.1 神经网络的例子

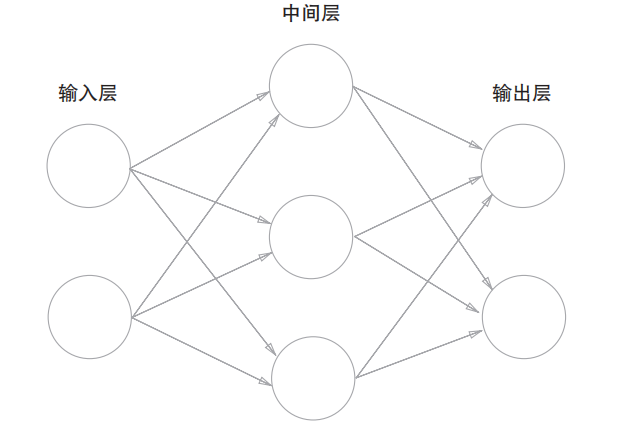
image-20260116145836157

这里涉及到一些概念:

  1. 输入层, 输出层.
  2. 中间层 (可以是多层叠加) 被称为隐藏层 (是一个黑盒子).
  3. 按照作者的约定, 从左输入层开始为 第 0 层 (不计入层数的计算中), 然后一次是第 1 层, 第 2 层, ...

3.1.2 复习感知机

这里也是一些概念的说明. 首先将单个感知机抽象成数学描述:

y={0(b+w1x1+w2x2)≤01(b+w1x1+w2x2)>0
  • 其中 b 是偏置参数. 用于描述神经元被激活的容易程度 (相当于上一章中的 −θ).
  • 而 w1, w2 为各个信号的权重参数, 用于控制各个信号的重要性 (权重越高, 对应信号的作用越大).

为了将偏置也用图形的方式绘制出来, 就有了:

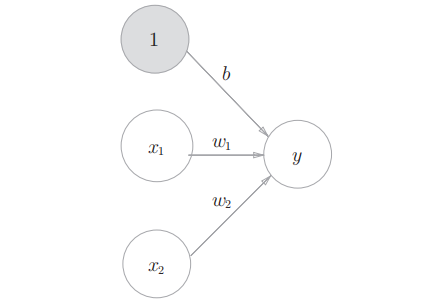
image-20260116150548103

将神经元的数学描述进一步抽象 (简化, 一般化), 引入激活函数 (activation function) h(x):

h(x)={0x≤01x>0

那么神经元的数学模型可以写成:

y=h(b+w1x1+w2x2)

3.1.3 激活函数登场

有了激活函数, 神经元模型可以画成:

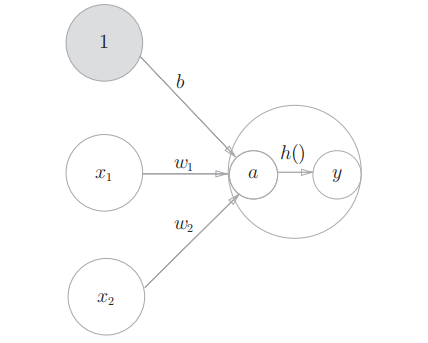
image-20260116151059827

这里偏置被视为信号值为 1, 权重为 b 的输入.

注意, 在本书中, 神经元, 节点等术语被视为一个含义.

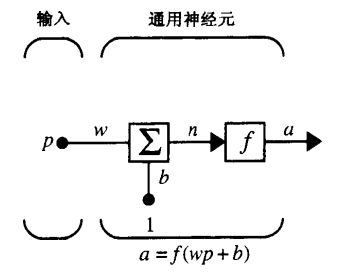
感觉学术型的黑皮书中表示更加科学严谨. 比如 "神经网络设计" 中将单个神经元描述为:

image-20260116151512812

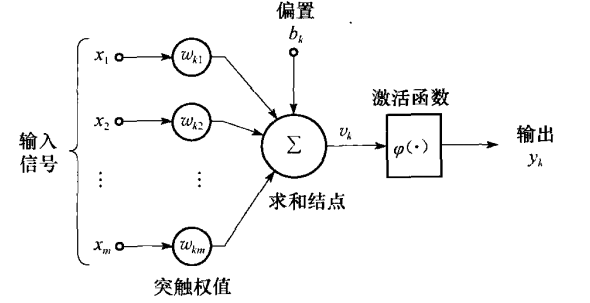
而 "神经网络与机器学习" 中将单个神经元绘制成:

image-20260116151639626

而 "神经网络原理" 中其表示与上图一样.

3.2 激活函数

3.2.1 阶跃函数

激活函数决定了输入信号的加权和是否可以激活当前神经元. 前面的示例中采用了阈值, 一旦超过阈值就激活. 这样的函数被称为 "阶跃函数". 函数图形似乎在跳跃一般. 例如:

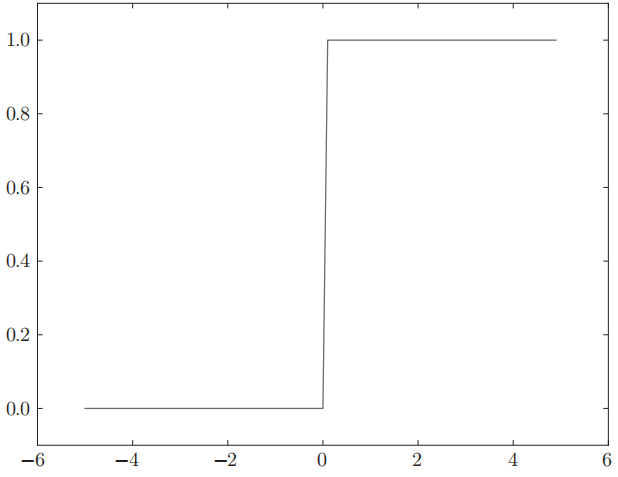
image-20260116152020906

其代码实现也很简单:

def step_function(x):
  if x > 0:
    return 1
  else:
    return 0

下面是 NumPy 版本:

def step_function(x): 
  '''x 是 NumPy 数组'''
  y = x > 0 # 会得到各个分量为 True/False 的数组
  return y.astype(np.int) # True -> 1/False -> 0

3.2.2 sigmoid 函数

神经网络中经常使用的一个函数:

h(x)=11+exp⁡(−x)

其中 exp⁡(−x) 函数表示 e−x 的含义, e 是纳皮尔常数: 2.7182⋯. 下面是 Python 的实现:

def sigmoid(x):
  return 1 / (1 + np.exp(-x))

该方法是支持 NumPy 数组的, 得益于其广播功能. 其函数图像为:

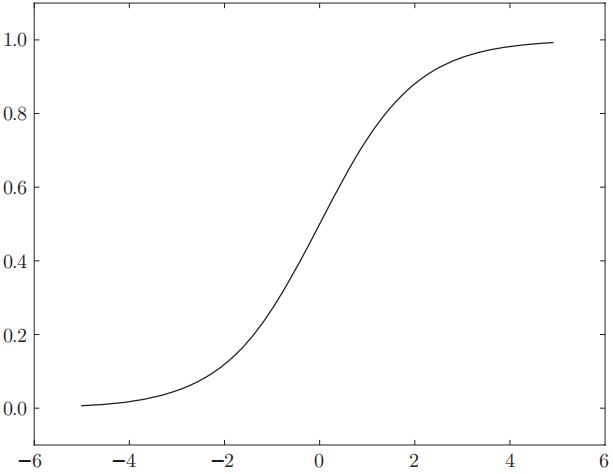
image-20260116155458351

3.2.3 非线性函数

无论是阶跃函数, 还是 sigmoid 函数, 它们都是非线性函数. 实际上, 神经网络的激活函数必须是非线性函数. 考虑到线性函数的定义: 线性组合的特性. 如果激活函数是一个线性函数, 那么无论多少层的神经网络, 都与一层没有区别. 也就失去了叠加的意义.

3.2.4 ReLU 函数

除了阶跃函数和 sigmoid 函数, 近些年常用的还有 ReLU 函数 (Rectified Linear Unit 函数):

h(x)={xx>00x≤0

其代码实现为:

def relu(x):
  return np.maximum(0, x)

其函数图像为:

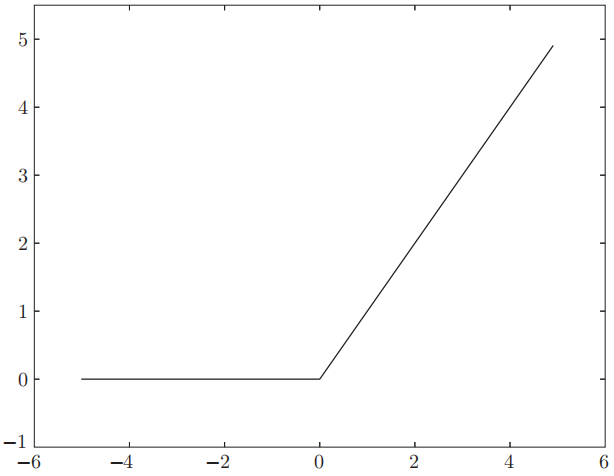
image-20260116160255927

作者表示, 本章剩余部分会继续使用 sigmoid 函数, 而本书的后半部分会使用 ReLU 函数.

3.3 多维数组的运算

3.3.1 矩阵乘法

首先主要介绍了矩阵 (matrix) 乘法:

  • 两个矩阵相乘, 是将左边矩阵的第 i 行, 与右边矩阵的第 j 列 中的元素依次相乘, 然后求和, 作为结果第 i 行, 第 j 列的元素.
  • 矩阵乘法通常不满足交换律.
  • 然后介绍用 NumPy 来实现矩阵乘法: np.dot(A, B).

同时补充了一个点, 就是 NumPy 数组的维度 np.ndim(A):

  • 可以将 NumPy 数组看成一个数组的数组.
  • 对于高维数组可以看成数组元素依旧为数组的数组.
  • 而其嵌套的层数即为其维度 (dimension). 并且维度的索引为 base-0 的. 从最外层开始编号.

实际上 np.ndim(A) 就是 np.shape(A) 返回元组的元素个数.

书中重点强调了矩阵的行列关系, 矩阵乘法中, 左矩阵的列数与右矩阵的行数必须相同.

3.3.2 神经网络的内积

将神经网络的计算与矩阵乘法关联起来:

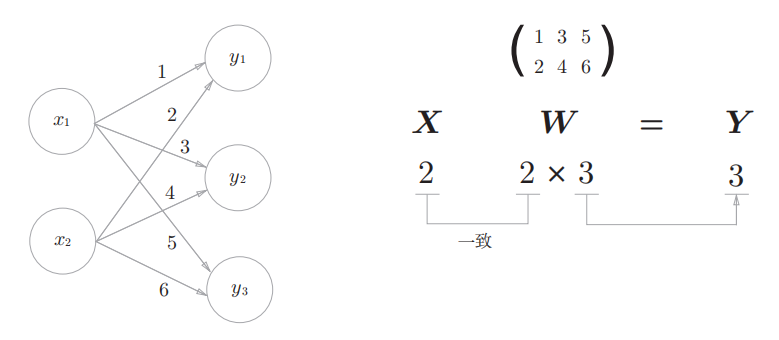
image-20260122095519376

将左边神经网络的权重依次列出来, 刚好构成一个矩阵.

  • 矩阵的行数, 为输入神经元的个数. 每一行, 表示一个神经元到下一个神经元的权重信息.
  • 而输入信号构成一个矩阵.
  • 将输入信号作为左矩阵, 权重作为右矩阵. 进行矩阵乘法, 刚好获得输出的信号信息 (不包含激活函数).

如此将神经网络计算归结为矩阵运算.

3.4+3.5 3 层神经网络的实现 + 输出层的设计

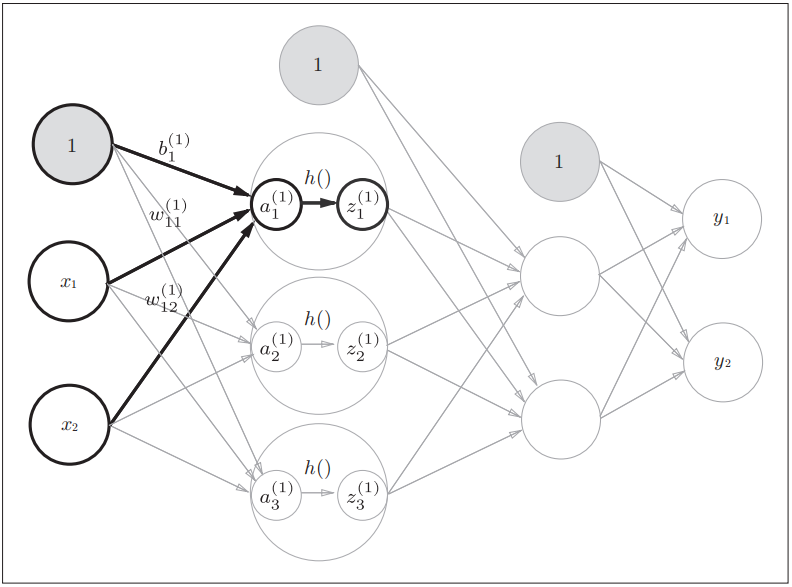
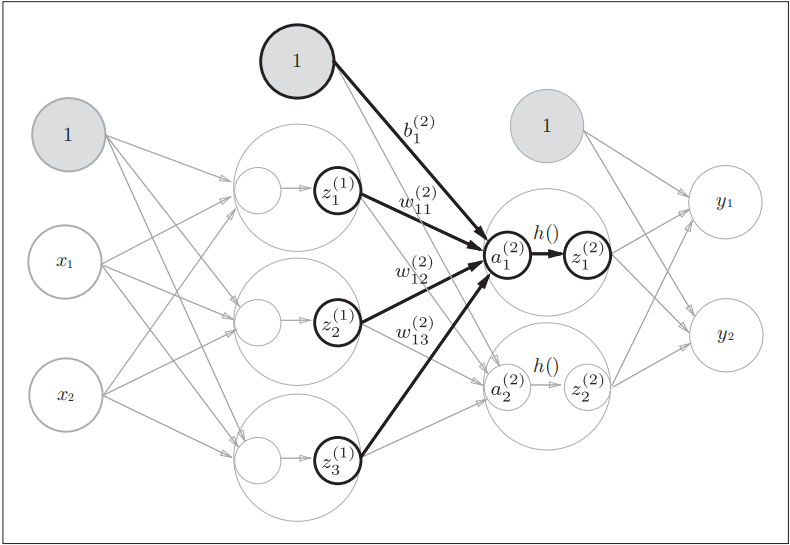
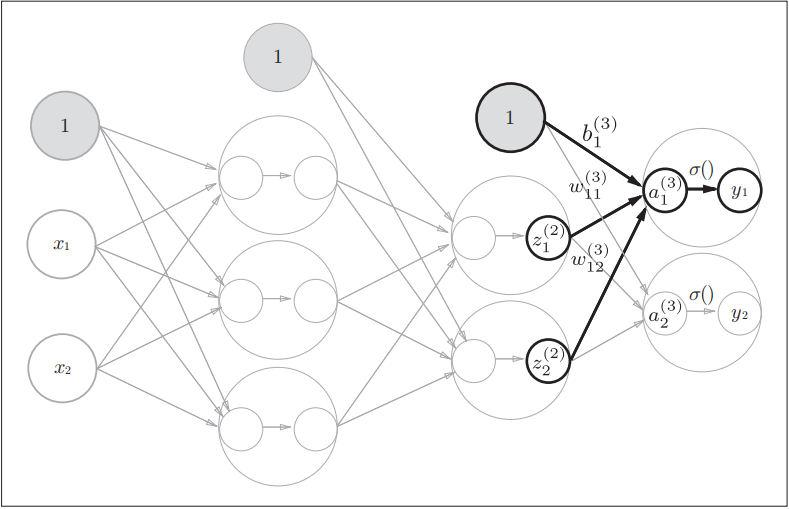
然后作者构造了一个三层神经网络, 来详细的解释如何利用矩阵将神经网络的计算表示出来.

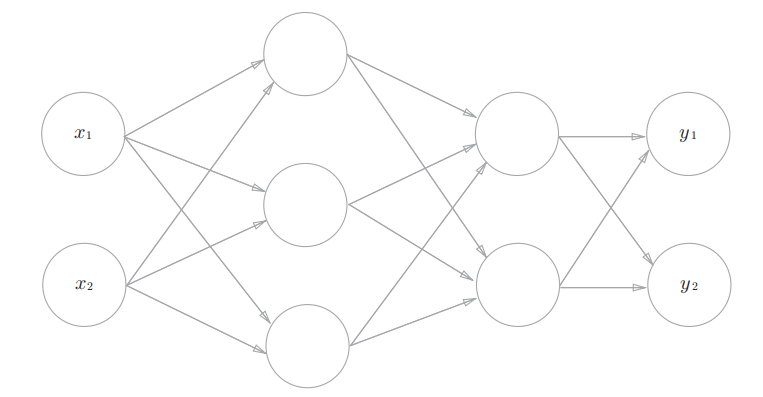
image-20260122095938615

这里比较基础, 不作展开(如果作为培训, 应该重点描述)

简单总结一下书中内容:

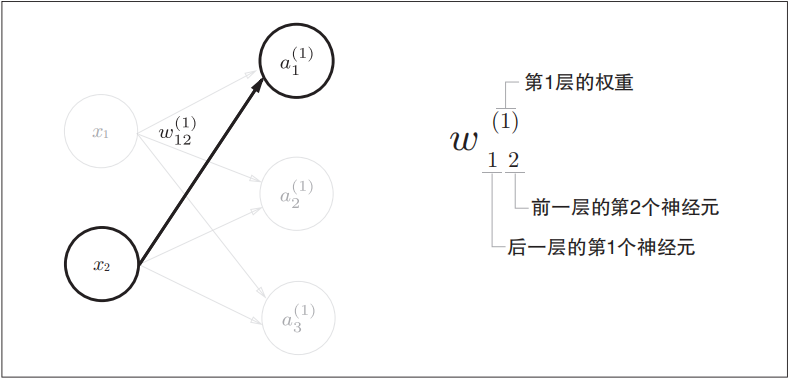
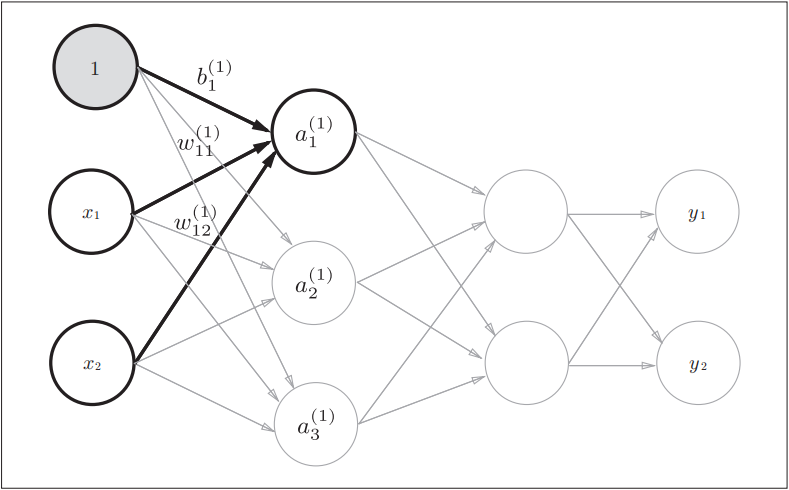
  1. 引入符号, 该符号为了适应数学中矩阵的下标描述, 将其与神经网络层, 前一个神经元序号, 后一个神经元序号等进行了关联.
  2. 作者选取一个神经元详细的进行了说明从输入层, 到输出层整个数据流转与计算.
  3. 并说明了激活函数: sigmoid 函数, softmax 函数, 以及恒等变换函数 (常用 σ 表示).
  4. 并对使用激活函数进行了小结:
    1. 回归问题的输出层可以使用恒等激活函数.
    2. 二分为题的输出层可以使用 sigmoid 函数. 隐藏层也可以使用 (不过现在更多使用 ReLU 函数)
    3. 多分类问题可以使用 softmax 函数 (该函数可以映射为概率).
  5. 然后对输出输入神经元的数量坐了说明
    1. 输入神经元是特征的表现, 有多少数据特征就有多少输入神经元.
    2. 输出神经元与结果挂钩, 如果判断是否, 即输出两个神经元; 若是识别数字 (0-9), 就是十个神经元.
  6. 利用代码封装了计算过程, 引入 forward 的概念. 将从输入层到输出层的顺序定义为向前处理.
  7. 并详细讨论了 softmax 函数在计算过程中存在的问题 ex 计算可能会溢出. 利用数学原理得到在计算时, 将所有参与计算的数据同时加上一个数字, 其计算结果不变. 因此在计算前会有一个预处理, 一般取数据集中的最大数, 然后让每一个数都减去该数字, 这样可以有效避免在计算时的溢出 (方法不唯一, 亦或平均数, 中位数等).
\begin{array}{rcl} y_k & = & \frac{\exp(a_k)}{\sum\limits_{i=1}^n\exp(a_i)} \\ & = & \frac{C\exp(a_k)}{C\sum\limits_{i=1}^n\exp(a_i)} \\ & = & \frac{\exp(a_k + \log C)}{\sum\limits_{i=1}^n\exp(a_i +\log C)} \\ & = & \frac{\exp(a_k + C')}{\sum\limits_{i=1}^n\exp(a_i +C')} \\ \end{array}

一些参考图:

image-20260122101657457

image-20260122101715735

image-20260122101727628

image-20260122101741531

image-20260122101801171

3.6 手写数字识别

这是使用了一个具体的案例, 来描述一个神经网络用代码如何实现, 并介绍了 MNIST 数据集.

这里作者的代码值得学习一下.

深度的应用流程上包含两部分:

  1. 学习, 也叫训练. 是建立神经网络, 并通过训练数据获得各个权重的过程.
  2. 推理. 就是利用学习生成的神经网络, 来对数据进行处理, 获得推理的结果.

推理的过程也称为神经网络的前向传播 (forward propagation).

早期使用 NumPy, 现在多半使用 PyTorch.

3.6.1 MNIST 数据集

MNIST 是机器学习领域最有名的数据集之一. 常用与简单试验与论文研究.

下面是数据集的描述:

  1. 数据集由 0 到 9 的数字图像构成.
  2. 训练图有 6 万张. 测试图有 1 万张.
  3. 图像数据是 28 x 28 像素的灰度图像 (1通道).
  4. 各个像素的取值在 0 到 255 之间.
  5. 每个图像数据响应的标有数字标签.

数据集类似于:

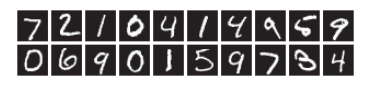
image-20260122113631171

使用 MNIST 数据的一般法:

  1. 首先使用训练集对模型 (构建的神经网络模型) 进行训练 (学习).
  2. 然后再使用生成的模型对测试数据进行推理. 判断该模型能达到多少的正确率.

使用随书代码

  1. 下载代码, 解压 (不要有中文路径)
  2. 用 PyCharm 直接在根目录打开文件夹, 建立基于项目的虚拟环境.
  3. 安装必要包 (README.md 中有描述, 按第一章安装下面软件):
    1. pip install numpy
    2. pip install matplotlib
    3. pip install jupyter

关于代码, 有一些补充说明:

Last Updated:
Contributors: jk