第二章 感知机
感知机 perceptron 有美国学者 Frank Rosenblatt 在 1957 年提出.
2.1 感知机是什么
- 感知机接收多个信号输入
- 输出一个信号
实际上就是对神经元的数学抽象. 感知机也就是神经元. 这里的信号为 0/1 两种取值.如图:
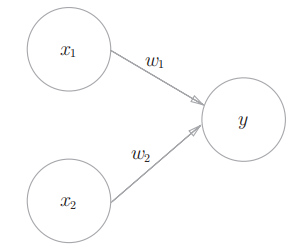
- 图中
- 不同的输入对应不同的权重, 分别用
- 最终输入信号与权重会分别相乘求和:
- 但是是否激活神经元, 即使得
因此有下面的结果:
每一个输入信号都会对应一个权重. 实际上训练过程实际上就是在计算确认这个权重的值.
2.2 简单逻辑电路
神经元的这种输入信号 + 权重 + 阈值的模型可以容易的设计成门电路.
作者分别描述了与门, 与非门, 和或门电路的结构. 同时给出一个重要的标准, 实际上是比较实际的真实的描述, 即不是数字化的结果, 而是模拟化的结果. 例如取 (不唯一)
实际上, 从具体的电路电气设备来看, 也并非是绝对的数字化, 比如单片机中对高低电平的定义, 如传统单片机约定
为高电平, 但事实上, 通常当电平拉高到 的时候就已经被视为高电平了. 而且电平的切换也不是阶跃的, 时间轴放大后也是慢慢变大的.
有关门电路的模拟这里不做说明, 仅说明结论:
- 使用单个神经元, 只能实现部分逻辑门.
- 使用多个神经元组合, 可以实现任意逻辑门.
- 根据计算机硬件接口原理, 只要有足够多的门电路, 就可以制造一台计算机, 所以理论上只要有足够的神经元, 就可以实现一台计算机.
2.3 感知机的实现
这里主要说明使用 Python 怎么在代码中模拟感知机. 并且使用门电路的方式来作为说明. 并基于 NumPy 工具来完成按权求和的过程. 这里仅整理算法注意项:
- 输入参数
x = np.array([x1, x2])表示. - 同理, 权重也可以表示为
w = np.array([w1, w2]). - 其优势是在 NumPy 中, 两个数组相乘, 是对应分量相乘. 即
x * w本质得到[x1 * w1, x2 * w2]. - 然后再使用
np.sum()求和, 就得到输入信号的加权和.
2.4 感知机的局限性
感知机的结果表达式本质上是输入信号的线性组合, 即它是线性函数, 那么逻辑上无法描述非线性特征.
- 作者依旧使用逻辑门来说明, 单个感知机无法实现异或门.
- 同时基于 2 个输入信号的神经元, 用平面几何的特性直观的描述了
最后的结论是: 感知机的局限性在于它只能表示一条直线分割的空间. 而曲线分割的空间是非线性的.
2.5 多层感知机
利用逻辑门的叠加 (组合), 构造无法直接实现的异或门. 引出感知机叠加的概念, 这便是多层感知机的雏形.
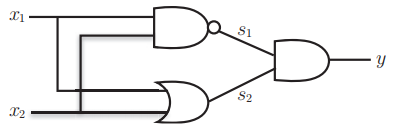
然后类比为:
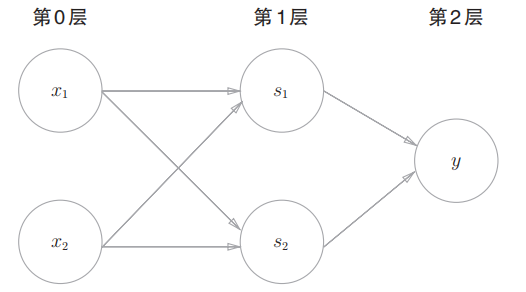
本书中有一个约定: 认知不同, 会造成描述的不一样. 如何定义多层感知机的层数是一个问题. 按照作者的描述, 具有权重的层才视为有效层, 因此作者将这个模型视为 2 层感知机模型.