附录A PyTorch 简介

主要提供必要的内容, 不是完整的介绍.

• 首先搭建一个支持 PyTorch 和 GPU 的深度学习平台.
• 介绍张量的基本概念, 以及在 PyTorch 中的用法.
• 深入 PyTorch 的自动微分引擎, 以供高效的使用反向传播.

A.1 什么是 PyTorch

它是基于 Python 的深度学习库. 它现在很流行.

A.1.1 PyTorch 的三大核心组件

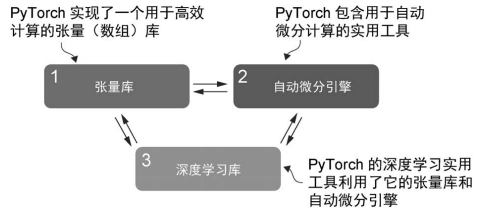
PyTorch 是一个全面的库. 可通过其三大核心组件来理解它.

• 首先, PyTorch 是一个张量库. 它扩展了 NumPy, 增加了 GPU 加速.
• 其次, PyTorch 是一个自动微分引擎, 也称为 autograd. 它可以自动计算张量梯度.
• 最后, PyTorch 是一个深度学习库. 它提供了模块化的构建块, 可以灵活的设计和训练各种模型.

A1.2 定义深度学习

大模型本质也是一种深度神经网络. 这里文中要对一些术语作一些说明.

然后书中描述了人工智能的目的(主要体现在智能上), 并解释了如今还远没达到预期. 然后解释了机器学习时人工智能的一个子集. 然后说明了深度学习的定位:

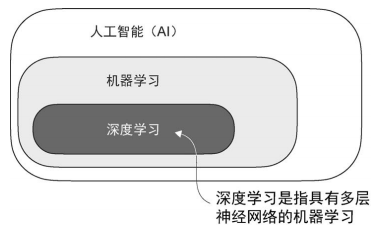
同时解释了各个领域的任务:

1. 机器学习专注于学习算法的开发与改进. 其主要理念是从数据中学习, 并在未明确编程的情况下进行决策与预测. 传统机器学习擅长简单的模式识别.
2. 深度学习专注于深度神经网络的训练和应用. 深度学习擅长处理图像, 音频, 文本等非结构化数据. 深度更适合大模型.

下图为机器学习与深度学习中典型的预测建模工作流程, 也被称为监督学习 (有既定目标).

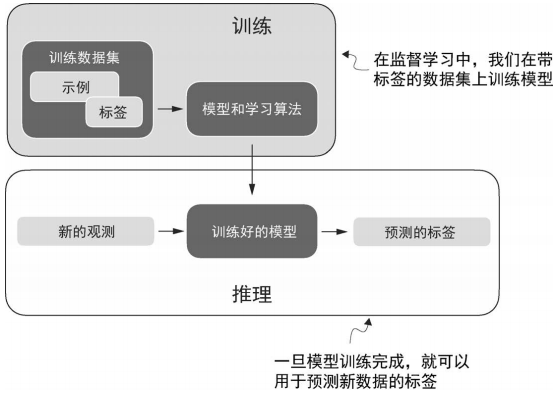
简单描述为:

1. 手机带有标签的数据.
2. 对该数据进行训练.
3. 可以识别既定标签.

然后作者用垃圾邮件作为示例, 解释了所谓的标签的含义. 同时如果使用大模型来对文本进行分类, 流程是类似的. 所以这个流程具有参考价值.

A1.3 安装 PyTorch

安装方式与其他 Python 包的安装方式一样. 只是因为其包含 CPU 和 GPU 的兼容代码, 需要补充一些说明.

• 科学计算的库一般不会支持最新的 Python, 因此建议在安装时, 选择比最新版本低一到两个版本的 Python.
• PyTorch 有两个版本:
  • 仅支持 CPU 的精简版
  • 支持 CPU 和 GPU 的完整版

如果有显卡, 则使用完整版, 安装命令为:

pip install torch

系统会根据现有环境自动选择安装. 书中的版本是 2.4.0, 为了保持与书的一致, 建议使用这个版本. 区别就是在 torch 后加上版本限制. 例如:

pip install torch==2.4.0

实际上访问官网的安装命令更为详细:

只需要注意在 torch 后加上版本号.

检查 torch 版本使用下面命令:

import torch
torch.__version__

关于 PyTorch 与 Torch 的说明:

由 Lua 创建的 Torch 是一个这机器学习的科学计算框架, 然后由 Python 扩展得到 PyTorch.

下面是一个安装参考, 基于 conda 环境:

conda create --name torch python==3.11
conda activate torch
pip install torch==2.4.0

使用下面命令可以查看是否支持 NVIDIA GPU:

import torch
torch.cuda.is_available()

如果不支持, 可以考虑云平台提供的 GPU 算力.

如果是 Mac 电脑, 下面命令可以检查是否具有支持加速 PyTorch 代码的 Apple Silicon 芯片.

print(torch.backends.mps.is_available())

torch 依赖于 numpy, torch 2.4.0 一来 numpy 1.X 的版本, 如果默认安装会提示不兼容. 使用下面命令安装:

pip install "numpy<2.0"

练习

两个任务:

1. 在本地安装 torch
2. 运行线上的补充代码

import torch

# --------------------------
# Onehot Encoding
def to_onehot(y, num_classes):
    y_onehot = torch.zeros(y.size(0), num_classes)
    y_onehot.scatter_(1, y.view(-1, 1).long(), 1).float()
    return y_onehot

y = torch.tensor([0, 1, 2, 2])

y_enc = to_onehot(y, 3)

print('one-hot encoding:\n', y_enc)

# ---------------------------
# one-hot encoding:
#  tensor([[1., 0., 0.],
#         [0., 1., 0.],
#         [0., 0., 1.],
#         [0., 0., 1.]])

# Softmax
Z = torch.tensor( [[-0.3,  -0.5, -0.5],
                   [-0.4,  -0.1, -0.5],
                   [-0.3,  -0.94, -0.5],
                   [-0.99, -0.88, -0.5]])

Z
# tensor([[-0.3000, -0.5000, -0.5000],
#         [-0.4000, -0.1000, -0.5000],
#         [-0.3000, -0.9400, -0.5000],
#         [-0.9900, -0.8800, -0.5000]])


# ----------------------------
def softmax(z):
    return (torch.exp(z.t()) / torch.sum(torch.exp(z), dim=1)).t()

smax = softmax(Z)
print('softmax:\n', smax)
# softmax:
#  tensor([[0.3792, 0.3104, 0.3104],
#         [0.3072, 0.4147, 0.2780],
#         [0.4263, 0.2248, 0.3490],
#         [0.2668, 0.2978, 0.4354]])

# ----------------------------
def to_classlabel(z):
    return torch.argmax(z, dim=1)

print('predicted class labels: ', to_classlabel(smax))
print('true class labels: ', to_classlabel(y_enc))
# predicted class labels:  tensor([0, 1, 0, 2])
# true class labels:  tensor([0, 1, 2, 2])

# -----------------------------
# Cross Entropy
def cross_entropy(softmax, y_target):
    return - torch.sum(torch.log(softmax) * (y_target), dim=1)

xent = cross_entropy(smax, y_enc)
print('Cross Entropy:', xent)
# Cross Entropy: tensor([0.9698, 0.8801, 1.0527, 0.8314])

# -----------------------------
import torch.nn.functional as F

F.nll_loss(torch.log(smax), y, reduction='none')
# tensor([0.9698, 0.8801, 1.0527, 0.8314])

F.cross_entropy(Z, y, reduction='none')
# tensor([0.9698, 0.8801, 1.0527, 0.8314])

F.cross_entropy(Z, y)
# tensor(0.9335)

torch.mean(cross_entropy(smax, y_enc))
# tensor(0.9335)

A.2 理解张量

张量 tensor. 数学中有一个张量分析, 看了很多年, 一直没进展, 惭愧 o(╯□╰)o...

张量是一个数学概念, 是统一 标量 (scale), 向量 (vector), 矩阵 (matrix), 高维度阵列的数据类型. 张量使用秩 (阶数) 来描述特征. 这个秩 (阶数) 就是维度.

• 标量, 一个数字, 不存在数字序列, 可以看成秩为 0 的张量.
• 向量, 是一维数字序列, 可以看成秩为 1 的张量.
• 矩阵, 是二维数字序列, 或向量的序列, 一个维度描述行, 一个维度表述列, 可以看成秩为 2 的张量.

需要注意的是三维向量也是秩为 1 的张量. 逻辑上是看秩的数量, 不是表征的维度数量.

直觉上, n 秩的张量对标一个编程结构中的 n 维数组. 书中, 作者将张量视为数据的容器.

PyTorch 张量类似于 NumPy 的数组. 并且其 API 从设计上也尽可能类似.

A.2.1 标量, 向量, 矩阵和张量

约定: 标量为 0 维张量, 向量为 1 维张量, 矩阵是 2 维张量, 更高维的直接用 n 维张量来描述.

使用代码 torch.tensor() 来创建 PyTorch 的 Tensor 类对象. 例如:

import torch
tensor0d = torch.tensor(1)
tensor1d = torch.tensor([1, 2, 3])
tensor2d = torch.tensor([[1, 2],
                         [3, 4]])
tensor3d = torch.tensor([[[1, 2], [3, 4]], 
                         [[5, 6], [7. 8]]])

A.2.2 张量的数据类型

默认为 64 位整数. 可以使用 .dtype 属性来访问数据类型: tensor.dtype.

会显示 torch.int64

如果使用浮点数来创建张量则会使用 32 位精度的浮点数类型 (torch.float32).

如此设计是为了权衡, 目的是尽可能节省资源, 加快模型训练速度:

• 32 位精度现在足够使用.
• 32 位消耗资源更少.
• GPU 架构对 32 位计算进行了优化.

如果要修改精度可以使用 .to() 方法. 例如: tensor.to(torch.float32)

A.2.3 常见的 PyTorch 张量操作

本书仅介绍涉及到的操作.

最早 torch 是基于 Lua 中实现的 view, 后有因为 NumPy, 实现了 reshape. 但还是有区别:

• view 要求数据在内存中是连续的. 否则无法工作. torch 中使用得更多.
• reshapre 在必要时会拷贝一份数据, 以满足内存布局的需求.

A.3 将模型视为计算图

下面看看 PyTorch 中的自动微分引擎. 又名 autograd. 它可以在动态计算图中自动计算梯度.

• 计算图是一种有向图, 用于 表达 和 可视化 数学表达式.
• 在深度学习下, 计算图列出了计算神经网络输出所需的计算顺序.
• 有了这个顺序, 可用于计算反向传播的梯度 (神网主要算法).

下面是一个具体的例子.

• 下面是一个逻辑回归分类器的前向传播(预测步骤).
• 将其看成一个单层神经网络.
• 它会返回一个 0 到 1 的分数.
• 计算损失时, 该分数会与真实的类标签进行比较.

import torch.nn.functional as F # 这是一个约定, 避免代码过长

y = torch.tensor([1.0]) # 真实标签
x1 = torch.tensor([1.1]) # 输入特征
w1 = torch.tensor([2.2]) # 权重参数
b = torch.tensor([0.0]) # 偏置单元
z = x1 * w1 + b # 网络输入
a = torch.sigmoid(z) # 激活和输出

lose = F.binary_cross_entropy(a, y)

二元交叉熵损失(Binary Cross-Entropy Loss, 简称BCE Loss)是深度学习中用于二分类问题的一种核心损失函数. 它通过衡量模型预测的概率值与真实标签(0或1)之间的差异, 来指导模型优化.

本示例的作用不在于代码实现, 重点是看怎么将一系列计算看成一个计算图.

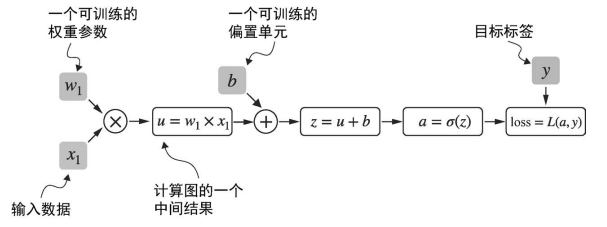
• 输入特征 x1 与 模型权重 w1 相乘.
• 然后加上偏置.
• 通过激活函数 $\sigma$ 传递.
• 损失时通过比较模型输出 a 与给定标签 y 来计算的.

实际上 PyTorch 在后台构建了一个这样的计算图, 可以利用该图来计算损失函数相对于模型参数 (这里是 w1 和 b) 的梯度, 从而训练模型.

有些迷惑. 似乎还是要有深度学习的一些背景, 但涉及到梯度, 损失函数什么的, 还要有优化, 机器学习的一些算法的背景.

这个计算图有点抽象语法树的感觉, 或指令集的感觉, 将一个计算表示为一个算法步骤.

A.4 轻松实现自动微分

若在 PyTorch 中计算, 主要在终端节点之一的 requires_grad 属性被设置为 true, PyTorch 就会在内部构建计算图. 而在训练神经网络时, 需要使用反向传播算法计算梯度 (微积分中链式法则在神经网络中的应用).

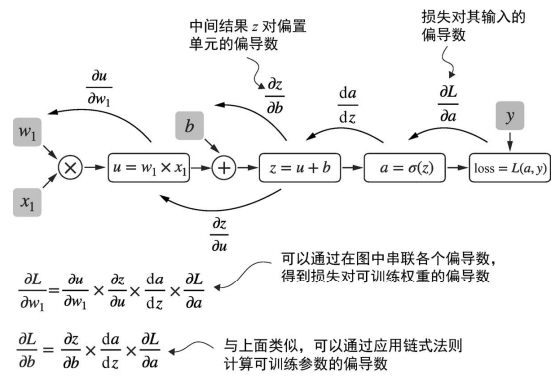
在计算图中计算损失梯度, 最常见的方法是从右向左应用链式法则 (反向模型自动求导, 反向传播).

所以说自右向左的计算损失函数的梯度就是反向传播?

偏导数和梯度

• 上图展示了偏导数, 它测量的是一个函数相对于其中一个变量变化的速率 (这是偏导数的定义).
• 梯度是一个向量 (是各个分量的偏导, 即各个分量的变化率).

微积分细节暂时不重要, 只需要知道 链式法则根据计算图来计算损失函数的梯度. 这个损失函数式衡量模型性能的代理.

PyTorch 的 autograd (自动微分) 引擎在后台跟踪在张量上的操作来构建计算图, 然后调用 grad 函数来计算损失相对于模型参数 w1 的梯度.

# 通过 autograd 计算梯度
import torch.nn.functional as F
from torch.autograd import grad

y = torch.tensor([1.0])
x1 = torch.tensor([1.1])
w1 = torch.tensor([2.2], requires_grad=True)
b = torch.tensor([0.0], requires_grad=True)

z = x1 * w1 + b
a = torch.sigmoid(z)

loss = F.binary_cross_entropy(a, y)

grad_L_w1 = grad(loss, w1, retain_graph=True)
grad_L_b = grad(loss, b, retain_graph=True)

默认, PyTorch 在计算梯度后会释放计算图, 由于两次使用该计算图, 在参数中使用 retain_graph=True, 保留该计算图. 那是不是第二个 grad 调用就不需要该参数了?

然后作者分别打印了损失函数相对于参数的梯度.

• 这里是手动调用 grad 函数完成的梯度计算. 这在调试, 演示等过程中很有用 (我可以理解成微调, 关注每一个步骤计算时的工具吗? 确实对调试友好).
• 在实际操作中, 可以对损失函数调用 .backward(), PyTorch 会计算计算图中所有叶节点的梯度, 并将其计算结果 (就是梯度) 存储与张量的 .grad 属性中.

所以上述操作, 可以简单写成 (这个简化, 计算步骤越多越明显):

loss.backward()
print(w1.grad)
print(b.grad)

作者作了一些微积分的说明与描述, 但对与不熟悉的读者不用在意, 只需要知道这个过程存在即可. 实际操作上一个 .backward() 即可完成.

话说要微调还是需要数学基础.

A.5 实现多层神经网络

上一个示例可以看成是一个单层神经网络, 下面是一个多层神经网络 (多层感知机 multilayer perceptron, 也称为全连接神经网络). 下面是一个具有两个隐藏层的多层感知机.

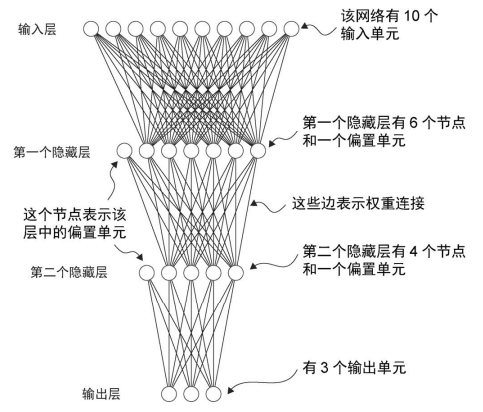
在 PyTorch 中实现神经网络时, 可以使用 torch.nn.Module 类 (它是一个基类) 来定义网络架构.

• 由该类派生子类 (我们所定义的神经网络), 在构造器 __init__ 中定义网络层数.
• 在 forward 方法中指定层与层之间的交互. 该方法中描述如何通过网络传递, 并形成计算图.
• 通常不用自己实现 backward.

下面是一个实例:

class NeuralNetwork(torch.nn.Module):
  def __init__(self, num_inputs, num_outputs):
    super().__init__()
    
    self.layers = torch.nn.Sequential(
      # 第一个隐藏层
      torch.nn.Linear(num_inputs, 30), # 线性层将输入节点和输出节点数量作为参数
      torch.nn.ReLU(), # 非线性激活函数被放在隐藏层之间
      
      # 第二个隐藏层
      torch.nn.Linear(30, 20), # 一个隐藏层输出节点数量必须与下一个输入层的数量一致
      torch.nn.ReLU(),
      
      # 输出层
      torch.nn.Linear(20, num_outputs),
    )
  
  def forward(self, x):
    logits = self.layers(x)
    return logits # 最后一层的输出称为 logits

然后实例化一个新的神经网络对象:

model = NeuralNetwork(50, 3)

可以使用 print(model) 来打印模型结构的摘要, 会出入如下:

在模型定义中使用了 Sequential, 这不是必须的, 但它是一个可以按照顺序执行的示例. 不用手动调用每一个层, 只需要在 forward 中调用 self.layers 即可.

可以理解为原本需要一个个手动调用, 但是这个操作比较泛化, 由 Sequential 实现了该泛化操作.

下面代码输出模型可训练参数的总数:

num_params = sum(p.numel() for p in model.parameters() if p.requires_grad)
print("可训练模型参数总数为: ", num_params)

• 每一个 requires_grad=True 的参数都会被视为可训练参数.
• 如上面讨论的神经网络模型, 可训练参数包含在 torch.nn.Linear 层中.
• Linear 层会将输入与权重作矩阵乘法, 然后加上偏置. 将其称为前馈层或全连接层.

根据 print(model) 的结构, 第一个 Linear 层在 layers 属性中的索引为 0, 如下可以访问权重矩阵:

print(model.layers[0].weight)

亦可使用 .shape 来显示其维度.

print(model.layers[0].weight.shape)

类似的也可以访问其偏置

print(model.layers[0].bias)

torch.nn.Linear 中默认会设置权重矩阵的 requires_grad=True, 即权重矩阵是可训练的.

注意, 模型权重会被小的随机数进行初始化. 这样可以在训练中打破对称性, 否则各个节点执行相同的操作, 并在反向传播中进行相同更新.

如果需要可重复的操作, 需要保证随机数可重现 (用于调试). 可以通过 manual_seed 来为 PyTorch 的随机数生成器设定种子.

torch.manual_seed(123)
model = NeuralNetwork(50, 3)
print(model.layers[0].weight)

下面看看怎么通过前向传播来使用该实例

torch.manual_seed(123)
X = torch.rand((1, 50))
out = model(X)
print(out)

• 上述代码中生成了一个 50 个数组成的一维向量 (由于使用了种子, 该随机数可复现)
• 然后传入神经网络中, 会得到 3 个分数 (模型的定义是 50 个输入参数, 3 个输出参数)
• 当调用 model(X) 时, 它会自动执行模型的前向传播 (即从输入张量开始到计算获得输出张量的过程).

输出结果类似于:

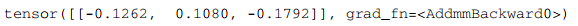
参数 grad_fn 表示计算图中用于计算某个变量的最后一个函数. PyTorch 会在反向传播中使用它. Addmm 表示它是一个矩阵乘法 (mm) 后接加法 (Add) 的组合运算.

若只使用网络进行预测, 而不进行训练或反向传播, 那么就不需要计算图. 因此在使用模型推理时, 最好使用 torch.no_grad() 上下文管理器, 即不用跟踪梯度:

with torch.no_grad():
  out = model(X)
print(out)

输出类似于:

在 PyTorch 中, 默认的做法是返回最后一层的输出 (logits), 而不是将这些输出传递给非线性激活函数. 这是因为: PyTorch 常用的损失函数会将 softmax (sigmoid, 二分类时) 操作与负对数似然损失 结合在一个类中. 这样可以提高数值计算的效率和稳定性.

实际上没读懂, 只知道是一个计算优化办法.

如果希望计算结果表示的是分类的概率, 需要显式调用 softmax 函数:

with torch.no_grad():
  out = torch.softmax(model(X), dim=1)
print(out)

输出形如:

至此它表示各个分类的概率, 其和约等于 1. 示例中这些值大致相等, 这是未经训练的随机数初始化的结果.

按照数学逻辑, 因为是随机初始化, 自然概率相同.

A.6 设置高效的数据加载器

数据加载器会在训练中迭代使用, 整体思路如下:

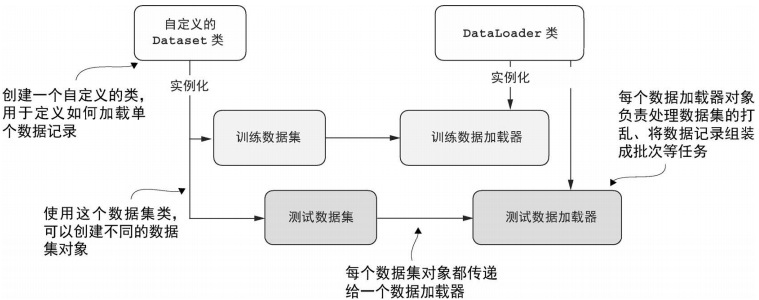
• PyTorch 实现了 Dataset 类与 DataLoader 类
• Dataset 定义如何加载数据
• DataLoader 负责打乱数据, 以及将数组组装成批次

下面基于 Dataset, 自定义训练数据集和测试数据集. 然后创建数据加载器.

首先要创建一个示例数据集:

1. 其中包含 5 个训练示例, 每个示例有两个特征.
2. 创建一个包含相应类别的标签张量
   1. 3 个示例属于类别标签 0
   2. 2 个示例属于类别标签 1
3. 构建一个包含两个样本的测试集

创建代码如下:

X_train = torch.tensor([
  [-1.2, 3.1],
  [-0.9, 2.9],
  [-0.5, 2.6],
  [2.3, -1.1],
  [2.7, -1.5]
]) # 训练示例
Y_train = torch.tensor([0, 0, 0, 1, 1]) # 标签张量

X_test = torch.tensor([
  [-0.8, 2.8],
  [2.6, -1.6],
]) # 样本测试集
Y_test = torch.tensor([0, 1]) # 样本测试集

PyTorch 中标签类别索引从 0 开始. 即标签类别有 0, 1, 2, 3, 和 4, 那么神经网络的输出层就应该有 5 个节点.

逻辑上还是应该有点神经网络的基础知识.

1. 上述代码中 X_train 是训练示例, 表示特征值范围. 有 5 个项, 表示有 5 个特征. 对标 5 个标签.
2. Y_train 是训练示例, 对标每一个特征的标签.

那么这个样本测试集的作用是啥? 现在还不清楚.

下面创建 ToyDataset:

from torch.utils.data import Dataset

class ToyDataset(Dataset):
  	def __init__(self, X, Y):
      self.features = X
      self.labels = Y
    
    def __getitem__(self, index):
      one_x = self.features[index]
      one_y = self.labels[index]
      return one_x, one_y
    
    def __len__(self):
      return self.labels.shape[0]
    
train_ds = ToyDataset(X_train, Y_train)
test_ds = ToyDataset(X_test, Y_test)

这些带有 __ 前后缀的方法, 是一个约定, len() 方法默认调用 __len__() 方法. [index] 默认调用 __getitem__(index) 方法.

下面使用 DataLoader 进行采样

from torch.utils.data import DataLoader

torch.manual_seed(123)

train_loader = DataLoader(
  dataset=train_ds,
  batch_size=2, # 训练批次大小
  shuffle=True, # 是否打乱数据
  num_workers=0 # 后台进程数量
)

test_loader = DataLoader(
  dataset=test_ds,
  batch_size=2,
  shuffle=False, # 测试数据集不需要打乱顺序
  num_workers=0
)

DataLoader 实例允许被迭代, 例如:

for idx, (x, y) in enumerate(train_loader):
  print(f"训练集 {idx + 1}: ", x, y)

实际上可以看成按 0 轴遍历 (shape 的返回值索引从 0 开始计算)

这个迭代会访问每一个训练示例一次, 被称为一个训练轮次. 由于设置了随机种子, 这个迭代顺序应该是不变的 (给人的感觉是, 迭代的顺序会是随机的, 亦或因为 shuffle=True 的原因, 猜测打乱的规则是基于随机数的).

但是再次迭代时会得到不同的顺序, 这是为了避免深度神经网络在训练过程中陷入重复更新循环.

batch_size 是训练批次大小, 行文中表示, 每次训练使用训练数据的数量. 这里批次大小为 2, 但训练数据有 5 个, 表示会分 3 次训练, 前两次都有 2 个示例, 第三次只有一个示例.

实践中, 如果最后一个批次的训练明显小于其他批次, 那么会影响到训练过程中的收敛. 可以设置 drop_last=True, 会在每一轮中丢弃最后一个批次.

train_loader = DataLoader(
  dataset=train_ds,
  batch_size=2,
  shuffle=True,
  num_workers=0,
  drop_last=True
)

如果再次迭代 for + enumeratie, 则会丢失最后一次迭代.

最后是 num_workers=0 参数. 该参数会影响到并行加载和预处理数据.

• 若为 0 表示数据加载在主进程中完成, 不会在单独的工作进程中. 但在 GPU 训练较大的网络时, 会很慢. 因为 GPU 需要等待 CPU (CPU 要加载数据, 预处理数据, 还要训练模型).
• 若取值大于 0, 则会启动多个工作进程并行加载数据, 从而释放主进程, 让主进程专注于训练模型.

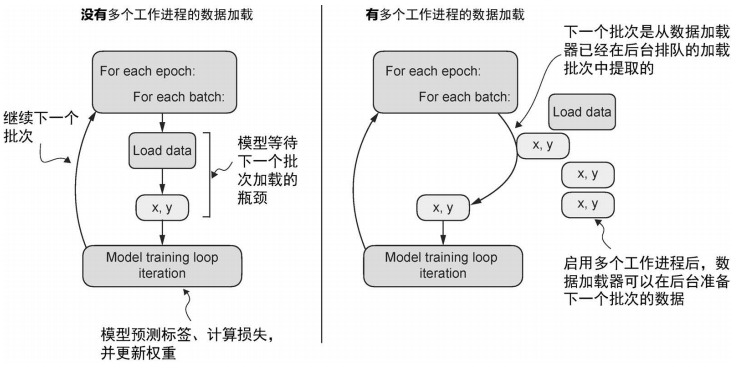
对于小数据集就不需要设置 num_workers, 因为开启后台进程可能比加载小数据集的资源消耗得更大.

显然大的网络并不适合使用交互式环境. 诸如 Jupyter Notebook, 设置后台进程还会因为进程资源共享问题导致错误, 甚至是崩溃.

根据作者经验, 实际训练时设置为 4 效果较理想, 但这也取决于硬件性能.

A.7 典型的训练循环

下面是在示例数据集上训练一个神经网络

import torch.nn.funtional as F

torch.manual_seed(123)
model = NeuralNetwork(num_inputs=2, num_outputs=2) # 该数据集有两个特征, 两个类别
optimizer = torch.optim.SGD(
  model.parameters(), lr=0.5 # 优化器需要知道哪些参数需要优化
)
num_epochs = 3
for epoch in range(num_epochs):
  
  model.train()
  for batch_idx, (features, labels) in enumerate(train_loader):
    logits = model(features)
    
    loss = F.cross_entropy(logits, labels)
    
    optimizer.zero_grad() # 将上一个梯度置 0, 防止意外梯度积累
    loss.backward() # 根据模型参数计算模型损失的梯度
    optimizer.step() # 优化器使用梯度更新模型参数
    
    ### LOGGING
    print(f"批次: {epoch + 1:03d}/{num_epochs:03d}"
          f" | 数据集 {batch_idx:03d}/{len(train_loader):03d}"
          f" | 训练损失: {loss:.2f}")
  
  model.eval()
  # 插入可选的模型评估代码

运行结果类似于:

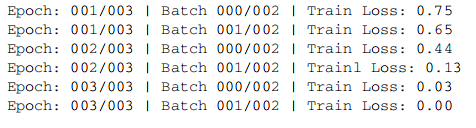
从结果上看, 损失在第 3 轮后降至为 0, 表示模型已在训练集上收敛.

• 这里初始化了一个具有 2 个输入和 2 个输出的模型. 因为我们的示例数据集有 2 个输入特征和 2 个类别标签需要预测. (猜测: 2 个输入特征是训练数据集 X_train 的 1 维分量是 2 个. 2 个分类是因为训练集标签有两个特征: 0 和 1).
• 这里使用了一个学习率 (lr) 为 0.5 的随机梯度下降 (RGD) 优化器.

理想状态下, 希望选择一个学习率, 使得损失在一定轮数后收敛 (轮数是另一个需要选择的超参数).

练习: 这个神经网络有多少个参数?

猜测:

• 训练集有两个, 一个是 shape 为 [n, m] 的 2 维张量; 一个是 shape 为 [n] 的 1 维张量.
• 这里 n 个数表示可以进行训练的数据次数, m 表示每次训练的参数个数.
• 如果映射到神经网络上, m 就表示入参个数.
• 而第二个训练集的 n 个数中, 去重后数据的个数, 即为需要分类的数量, 即神经网络中输出的个数.

在实际操作中, 会使用第三个数据集 (验证数据集), 来找最优的超参数. 验证集与测试集类似. 一般都会多次使用来验证集来调整模型参数.

• 代码中 model.train() 表示将模型置于训练模式.
• 代码中 model.eval() 表示将模型置于评估模式.

由于代码中没有涉及一些深入的内容, 这里没什么区别 (深入还是需要建立深度学习的技术背景). 作者建议在编写代码时, 按照完整的模式进行编码, 以便在后期维护, 调整时兼容性更好.

然后作者对代码进行了解释说明, 这些对有深度背景的不用考虑, 对于没有这些背景的也说不清楚, 这里略去.

训练好模型后, 可以使用它进行预测:

model.eval()
with torch.no_grad():
  outputs = model(X_train)
print(outputs)

结果类似于:

为了获得成员率, 可以使用 softmax 函数:

torch.set_printoptions(sci_mode=False) # 使得代码易于阅读
probas = torch.softmax(outputs, dim=1)
print(probas)

运行结果类似于

这里一第一行为例, 第一列表示训练示例属于标签 0 的概率为 99.91%, 属于标签 1 的概率为 0.09%.

也可以使用 argmax 函数将这些概率值转换为类别标签预测, 若设置 dim=1, 则会返回每行中最大值的索引位置, 设置 dim=0, 返回每列中最大值的索引位置.

predications = torch.argmax(probas, dim=1)
print(predications)

得到:

注意, 如果只是为了获得类别标签, 计算 softmax 概率可以省略, 直接对 logits 应用 argmax 函数:

predications = torch.argmax(outputs, dim=1)
print(predictions)

输出结果一样. 实际上由于数据集很小, 可以直接看出结果. 但也可以使用 == 将结果与训练集作比较:

predications == Y_train

运行结果类似于:

用 torch.sum 可计算出正确数量: torch.sum(predications == Y_train), 输出为 5. 为了使预测准确率的计算更加通用, 可以封装一个 compute_accuracy 函数:

def compute_accuracy(modal, dataloader):
  model = model.eval()
  correct = 0.0
  total_examples = 0
  
  for idx, (features, labels) in enumerate(dataloader):
    
    with torch.no_grad():
      logits = model(features)
      
    predictions = torch.argmax(logits, dim=1)
    compare = labels == predictions # 根据标签是否匹配, 返回一个 True/False 张量
    correct += torch.sum(compare)
    total_examples += len(compare)
  
  return (corrent / total_examples).item() # 正确率的比例是一个介于 0 到 1 的值, .item() 会将张量的值以 Python 浮点数的形式返回.

可以将该方法用于训练数据, 类似的, 也可以用于测试数据

print(compute_accuracy(model, train_loader))
print(compute_accuracy(model, test_loader))

A.8 保存与加载模型

保存模型到本地磁盘使用代码:

torch.save(model.state_dict(), "model.pth")

• state_dict 是一个字典对象, 它将模型的每一层映射到其可训练的参数 (权重和偏执)
• 文件名与后缀可以随意使用, 但后缀一般约定为 pt 或 pth.

从磁盘恢复模型使用代码:

model = NeuralNetwork(2, 2)
model.load_state_dict(torch.load("model.pth"))

注意模型的入参与出参数量.

A.9 使用 GPU 优化性能

• 首先了解主要概念
• 然后在单个 GPU 上训练
• 最后讨论在多个 GPU 上进行分布式训练

A.9.1 在 GPU 设备上运行 PyTorch

只用修改 3 行代码, 就可以修改训练循环可以在 GPU 上运行. 在 PyTorch 中设备是计算和存储数据的地方. GPU 和 CPU 都是设备. 如果 PyTorch 张量存放在某个设备上, 其操作也会在该设备上执行.