ch15 动态规划 - 1. 钢条切割问题

动态规划 (dynamic programming), 常常简称为 DP.

动态规划是通过组合子问题来求解原问题的方法 (必然出现递归逻辑, 子问题与原问题存在形式相同的需求).

这里的 programming 不指编程, 而是指表格化.
传统递归效率低下, 主要是因为重复计算某些子问题, 这里在计算过程中, 将计算过的子问题进行缓存 (形成表格), 再次遇到该子问题时, 查表即可. 从而提升递归效率.

动态规划一般用于求解最优化问题 (optimization problem).

这类问题一般有很多解.
每一个解都有一个值.
希望求得一个最优值 (最大或最小).

将这个解称为一个最优解 (the optimal solution) (可能有多个最优解).

一般设计一个动态规划算法需要 4 个步骤:

刻画一个最优解的 结构特征.
递归定义最优解的值.
计算最优解的值. 一般采用自底向上的方法.
利用计算出的信息构造一个最优解.

抽象. 真是太抽象了.
这里最优解的值, 表示那个最值, 即最大/小的值.
而解本身, 是一个方案, 即选取, 或采纳的组合方式, 用这个方式计算出最后的值是这个最值. (所以解是存在一定结构的).

如果仅需要值, 只需要前3个步骤; 如果需要解本身, 就需要最后一个步骤了.

本章使用的案例:

钢条切割案例, 要求总价值最大.
矩阵链乘法结合方式, 来使得进行标量乘法的次数最少.
寻找最长子序列.
构造最优搜索二叉树.

本章的一个思路:
简要说明什么是 DP 算法, 以及其操作步骤 (是真抽象).
然后给定两个示例 (钢条切割, 矩阵链乘法), 来按照这个步骤操作, 演示具体的步骤.
然后介绍方法论, 给出抽象的描述.
再给定两个案例, 按照抽象的描述进行处理, 来巩固抽象化的描述.

钢条切割问题

给出一根钢条, 切割后售卖, 要求利润最高.

基本条件:

一根钢条, 切法待定.
一个表格, 钢条长度与价格的关系, 用于计算利润.

所以基本条件中需要明确一个规则, 就是要求的最优值, 需要一个可计算的表达式. 这里的表格起到这个作用.

问题描述:

给定一段长度为 $n$ 的钢条和一个价格表 $p_{i} (i = 1, 2, 3, \dots, n)$ , 求切割方案, 使得营收 $r_{n}$ 最大.

注意, 可能不需要切割.

价格 $p_{i}$ 代表 price, 利润 $r_{n}$ 大概表示 return.

表格示例:

长度 $i$	1	2	3	4	5	6	7	8	9	10
价格 $p_{i}$	1	5	8	9	10	17	17	20	24	30

计算中使用这个价格表来演示算法.

然后要总结归纳, 作者将问题尽可能转换为一个递推关系. 将切割 $n$ 的问题转换为切割 $n - 1$ 的问题.

作者选择了 $n = 4$ 的钢条进行不完全归纳.

我在想, 是不是可以考虑其他的情况? 比如 $n = 3$ , 如果 $n = 5$ 情况多了不好演算.
通过表格, 可知 $n = 3$ 不切收益最高, 所以最小的可讨论的 $n = 4$ . $n = 5$ 也可以讨论, 只是太复杂, 有 $16$ 种方案, 不过可以考虑转换为子问题, 寻找规律.

切割长度是整数段 (价格表是整数的), 所以穷举所有的切割方案:

全切成 1 的
包含 2 的, 1 个 2 的, 2 个 2 的
包含 3 的
包含 4 的 (不切)

穷举后

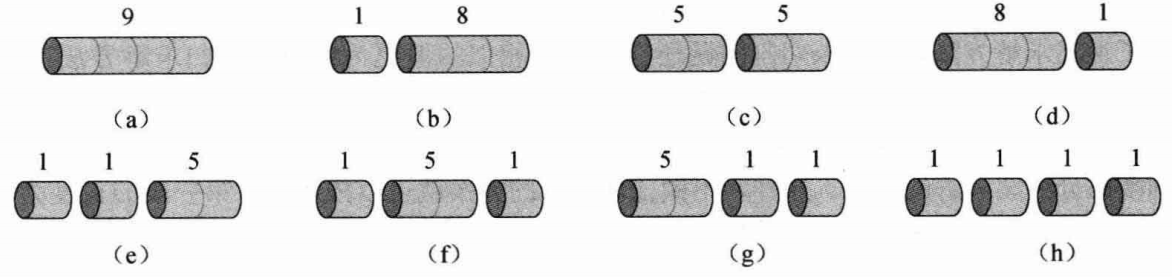
将收益标在上方.

穷举所有的可能有 $2^{n - 1}$ 种可能 (最多).

由于是求收益, 而切割后的收益金额求和得到, 加法满足交换律, 所以切法: $1 + 3$ 与 $3 + 1$ 的切法所得到的收益是一样的. 再没有确定该收益不是最高时, 应该同时考虑这两种切法. 那么得到的最优解可能不唯一.

但是该算法最终会发现, 最优解是唯一的, 因此在处理这个特殊的长度切割方案时, 可以按照作者在脚注中描述的, 可以按照长度递增的方案来整理切割分组. 这样将 $1 + 3$ 和 $3 + 1$ 视为同一个方案, 考虑的情况将会减少很多. 这个可以在后期优化时考虑.

很明显, 从切割的方案来看, 方案 c 是最优方案.

若将长为 $n$ 的钢条切成 $k$ 段, 每段长度为 $i_{m}, m = 1, 2, \dots, k$ . 基于表格 (一个长度到收益的函数), 分别对应的价格为 $p_{m}, m = i_{1}, i_{2}, i_{3}, \dots, i_{k}$ . 有

n = i_{1} + i_{2} + \dots + i_{k}

获得的收益 $r_{n}$ (下标用于描述钢条长度) 为

r_{n} = p_{i_{1}} + p_{i_{2}} + \dots + p_{i_{k}}

基于该数学模型, 通过观察列表

钢条长度	最优切割方案	收益
$n = 1$	$1 = 1$ (不切割)	$r_{1} = 1$
$n = 2$	$2 = 2$ (不切割)	$r_{2} = 5$
$n = 3$	$3 = 3$ (不切割)	$r_{3} = 8$
$n = 4$	$4 = 2 + 2$	$r 4 = 5 + 5 = 10$
$n = 5$	$5 = 3 + 2$	$r_{5} = 8 + 5 = 13$
$n = 6$	$6 = 6$ (不切割)	$r_{6} = 17$
$n = 7$	$7 = 1 + 6$ 或 $7 = 2 + 2 + 3$	$r_{7} = 1 + 17 = 5 + 5 + 8 = 18$
$n = 8$	$8 = 2 + 6$	$r_{8} = 5 + 17 = 22$
$n = 9$	$9 = 3 + 6$	$r_{9} = 8 + 17 = 25$
$n = 10$	$10 = 10$ (不切割)	$r_{10} = 30$

通过穷举可能性, 来寻找规律, 抽象出子问题. 作者只是没有在书面中描述出来. 给出表格, 实际上表示已经讨论了它的切割方案. 所以在抽象的时候可以通过穷举出来寻找规律.

然后作者提出一个观点: 原问题转换成子问题来处理. 即可以使用更短的钢条的最优解来描述当前钢条的最优解.

长度为 $n$ 的钢条切割收益为 $r_{n}$ .
如果不切割, 收益为 $p_{n}$ .
将其转换为子问题, 可能的子问题按照长度划分为 2 段:
- 长度为 $1$ 和 $n - 1$ , 对应收益为 $r_{1}$ 和 $r_{n - 1}$ .
- 长度为 $2$ 和 $n - 2$ , 对应收益为 $r_{2}$ 和 $r_{n - 2}$ .
- ... ...
- 长度为 $n - 1$ 和 $1$ , 对应收益为 $r_{n - 1}$ 和 $r_{1}$ .

上述的可能性就是长度为 $n$ 的子问题, 那么收益可以写成递推关系:

r_{n} = max (p_{n}, r_{1} + r_{n - 1}, r_{2} + r_{n - 2}, \dots, r_{n - 1} + r_{1})

求解一个规模为 $n$ 的原问题, 先求解形式完全一样, 但规模更小的问题. 这将切割长度为 $n$ 的钢条, 转换成两个相关的子问题来求解. 由于无法预知那种最优, 所以穷举子问题后求最大 ( $max$ ). 从而解答原问题.

引入一个新概念: 最优子结构 (optimal substructure): 问题的最优解由相关的子问题的最优解组合而成, 这些子问题可以独立求解.

可见钢条切割是满足最优子结构的.

另一个方案

除了上面介绍的方案, 还有另一个简单的递归方案: 从左端切下长为 $i$ ( $i \leq n$ ) 的一段, 将剩下剩下长为 $n - i$ 的一段继续切割 (构成子问题递归处理), 左边的一段不再切割.

如此不切割方案可以描述为: 长度为 $n$ 的钢条, 从左侧切下长为 $n$ 的一段, 收益为 $p_{n}$ , 然后剩下长为 $0$ 的一段, 不用切割, 收益为 $0$ .

如此可以将收益描述为:

r_{n} = max_{1 \leq i \leq n} (p_{i} + r_{n - i})

这个 $r_{n - i}$ 就构成子问题的结果, 构成了递归关系.

求解 DP 问题 (递归方法) 有另种方式:

自顶向下的方法 (从 $n$ 开始计算, 求到临界值, 例如 $1$ , 遇到需要子问题求解是压栈).
自底向上的方法 (从临界值, 例如 $1$ , 开始计算, 计算到 $n$ ).

自顶向下的方法 (朴素递归算法)

根据上面的递推关系, 编写算法:

cut_rod(p, n):
	if n == 0:
		return 0
	q = -infinity
	for i = 1 to n:
		q = max(q, p[i] + cut_rod(p, n - i))
	return q

其中参数 p 是价格表, 描述钢条长度 i 与价格 p[i] 的映射. 单纯分析算法, 可以不考虑该参数.
当切到不用再切时结束, 这里的临界值为 $0$ .

由于不确定怎么且才能最优, 所以按照从 1 到 n 的依次来一遍, 取最大的. 取最大的算法:

q = -1; // 由于价格都是正数, 可以这么操作
for i = 1 to:
  if q < p[i] + 子问题收益:
    q = p[i] + 子问题收益

该操作会压栈, 当 $n = 4$ 时的调用树为

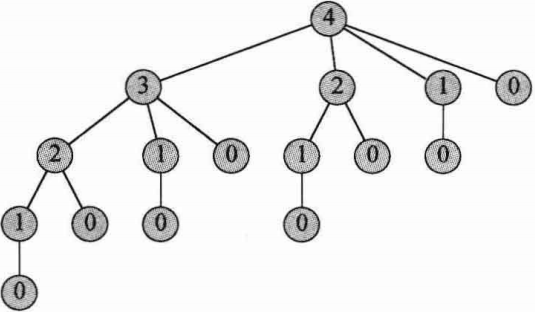
然后树中简要分析了该数的形成原因. 可见每一个子问题会反复被求解.

一般来说, 这棵递归树有 $2^{n}$ 个节点, 有 $2^{n - 1}$ 个叶子节点.

一般分析算法的时间, 使用利用某个执行次数来判断的.

实际上这是递归的通病, 子问题会反复入栈出栈.

要分析运行时间, 令 $T (n)$ 表示执行 cut_rod(p, n) 的次数.

p 不作考虑.

当 $n = 0$ 时, 函数只会调用一次, 即 $T (0) = 1$ .

而在函数内部可以知道, 函数内部会依次调用 cut_rod(p, n - 1), cut_rod(p, n - 2), ..., cut_rod(p, n - n). 因此调用一次该函数, 该函数会执行:

T (n) = 1 + \sum_{j = 0}^{n - 1} T (j)

练习: 根据 $T (0) = 1$ , 证明 $T (n) = 2^{n}$ .
2024年8月22日不会做.

可见其时间是按指数增长的, 非常可怕.

使用动态规划算法来求解

递归问题是定了. 问题在于怎么计算减少递归次数, 拿空间换时间, 用缓存, 使得子问题只计算一次, 再次遇到查表取结果. 所以有两种方案:

带缓存的自顶向下方法 (to-down with memorization).
自底向上方法 (bottom-up method). 推荐使用该方法.

带缓存的自顶向下方法

memoized_cut_rod(p, n):
	r[0..n] := [-1, ...] // 初始化缓存, 因每一个 n 会得到一个最优解, 
	                     // 用长度为 n 的存储空间来缓存数据,
	                     // 因要求最大值, 使用赋值或负无穷来初始化该存储空间.
	                     // 也可以根据情况存储 null, 只要后面可以判断其中是否有值
	return memorized_cut_rod_aux(p, n, r)

memorized_cut_rod_aux(p, n, r):
  if r[n] >= 0:        // 判断存在
    return r[n]
  if n == 0:
    q = 0
  else 
    q = -infinity
    for i = 0 to n:
      q = max(q, p[i] + memorized_cut_rod_aux(p, n - i, r))
  r[n] = q
	return q

转换为 C# 代码 (可运行):

namespace Demo;

public class Demo1 {
  public static Dictionary<int, int> p = new () {
    { 1, 1 }, { 2, 5 }, { 3, 8 }, { 4, 9 }, { 5, 10 }, 
    { 6, 17 }, { 7, 17 }, { 8, 20 }, { 9, 24 }, { 10, 30 }, 
  };

  public static double MEMORIZED_CUT_ROD(
    Dictionary<int, int> p, int n
  ) {
    var r = new double[n + 1];
    for (var i = 0; i < r.Length; i++) {
      r[i] = double.NegativeInfinity;
    }
    return MEMORIZED_CUT_ROD_AUX(p, n, r);
  }

  public static double MEMORIZED_CUT_ROD_AUX(
    Dictionary<int, int> p, int n, double[] r
  ) {
    if (r[n] >= 0) return r[n];
    if (n == 0) return r[0] = 0;
    double q = double.NegativeInfinity;
    for (var i = 1; i <= n; i++) {
      double next = p[i] + MEMORIZED_CUT_ROD_AUX(p, n - i, r);
      if (q < next) q = next;
    }
    return r[n] = q;
  }
}

然后演示运行代码:

for (var i = 0; i < 11; i++) {
  var res = Demo1.MEMORIZED_CUT_ROD(Demo1.p, i);
  System.Console.WriteLine("n = {0}, r_{1} = {2}", i, i, res);
}

得到的运行结果为:

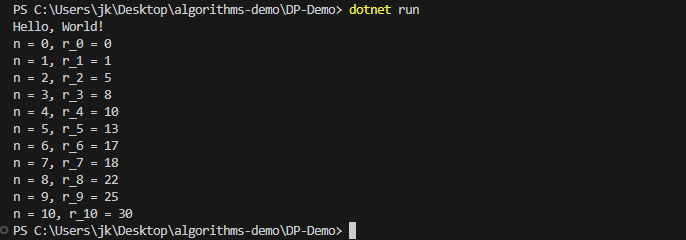
自底向上方法

自顶向下有大量压栈, 所以 DP 问题常被转换为自底向上的处理办法:

BOTTOM_UP_CUT_ROD(p, n):
  r[0..n]
  r[0] = 0
  for j = 1 to n:
    q = -1
    for i = 1 to j:
      q = max(q, p[i] + r[j - i])
    r[j] = q
  return r[n]

实际上如何将递归算法转换为自底向上的算法还是有一定难度的.

作者对该算法进行了简要解释.

自底向上, 所以优先考虑使用短的钢管的切割方案. 所以切割方法从 $0$ 开始, 到给定钢管 $n$ . 这就有了第一层循环. 以及 r[0] = 0 的处理结果.
而对于长为 $j$ 的钢管, 从到左边长为 $i$ 的位置进行切割, 那么就会切成两段长为 $i$ 和 $j - i$ 的钢管.
由于从小的长度开始切割, 优先会考虑 $0$ , 然后是 $1$ , $2$ , ..., 如此 $i$ 段可以通过查表 (p 表) 获得对应的价格.
另一端长为 $j - i$ 的可以使用递归, 所以有表达式 p[i] + r[j - i], 其中 r[j - i] 则利用递归来计算.
补充:
优先遍历 $j$ , 作为起点 $j = 0$ 是 $0$ .
然后当 $j = 1$ 时, 考虑 $i$ 的取值也从 $1$ 开始, $r [j - i]$ 相当于 $r [0]$ , 此时该值已存在了.
然后处理 $j = 2$ 是, $i$ 依次取 $1$ , $2$ , 那么需要计算的是 $r [j - i]$ , 即 $r [1]$ 和 $r [0]$ . 而上一步中, 该值已存在.
因此自底向上的方法可以将递归移除.
有点尾递归优化成迭代的感觉.

然后说明了这两种方法有相等的渐进运行时间.

可运行的代码:

namespace Demo;

public class Demo2 {

  public static Dictionary<int, int> p = new () {
    { 1, 1 }, { 2, 5 }, { 3, 8 }, { 4, 9 }, { 5, 10 }, 
    { 6, 17 }, { 7, 17 }, { 8, 20 }, { 9, 24 }, { 10, 30 }, 
  };

  public static double BOTTOM_UP_CUT_ROD(
    Dictionary<int, int> p, int n
  ) {
    double[] r = new double[n + 1]; //
    r[0] = 0;
    for (var j = 1; j < n + 1; j++) {
      double q = double.NegativeInfinity;
      for (var i = 1; i < j + 1; i++) {
        double next = p[i] + BOTTOM_UP_CUT_ROD(p, j - i);
        if (q < next) q = next;
      }
      r[j] = q;
    }
    return r[n];
  }

}

优化后的代码:

namespace Demo;

public class Demo2Ext {

  public static Dictionary<int, int> p = new () {
    { 1, 1 }, { 2, 5 }, { 3, 8 }, { 4, 9 }, { 5, 10 }, 
    { 6, 17 }, { 7, 17 }, { 8, 20 }, { 9, 24 }, { 10, 30 }, 
  };

  public static double BOTTOM_UP_CUT_ROD(
    Dictionary<int, int> p, int n
  ) {
    double[] r = new double[n + 1]; //
    r[0] = 0;
    for (var j = 1; j < n + 1; j++) {
      double q = double.NegativeInfinity;
      for (var i = 1; i < j + 1; i++) {
        double next = p[i] + r[j - i];
        if (q < next) q = next;
      }
      r[j] = q;
    }
    return r[n];
  }

}

其他代码不用修改, 只用调整计算 j - i 的切法.
将 double next = p[i] + BOTTOM_UP_CUT_ROD(p, j - i); 修改为 double next = p[i] + r[j - i];

子图问题 (暂略)

重构解

上述算法中仅能求解出最终的收益, 如果需要记录切割方法, 以自底向上方法为例, 需要记录在长度为 $n$ 的钢条左边切割的长度 $i$ 的值. 即:

EXTENDED_BOTTOM_UP_CUT_ROD(p, n):
  r[0..n], s[0..n]     // 用 s[0..n] 记录切割方案
                       // 原问题转换为两个子问题来处理, 所以给出的方案都是左边的切法. 
                       // 左边切法有了后, 右边的切法利用查表即可获得.
  r[0] = 0
  for j = 1 to n:
    q = -infinity
    for i = 1 to j:
      if q < p[i] + r[j - i]
        q = p[i] + r[j - i]
        s[j] = i // 长度为 j 的钢管, 距离左边 i 的距离切割
    r[j] = q
  return r, s

详细算法为:

namespace Demo;

public class Demo3 {

  public static Dictionary<int, int> p = new () {
    { 1, 1 }, { 2, 5 }, { 3, 8 }, { 4, 9 }, { 5, 10 }, 
    { 6, 17 }, { 7, 17 }, { 8, 20 }, { 9, 24 }, { 10, 30 }, 
  };

  public static (double[], double[]) EXTENT_BOTTOM_UP_CUT_ROD(
    Dictionary<int, int> p, int n
  ) {
    double[] r = new double[n + 1];
    double[] s = new double[n + 1];
    r[0] = 0;
    for (var j = 1; j < n + 1; j++) {
      double q = double.NegativeInfinity;
      for (var i = 1; i < j + 1; i++) {
        double next = p[i] + r[j - i];
        if (q < next) {
          q = next;
          s[j] = i;
        }
      }
      r[j] = q;
    }
    return (r, s);
  }
}

运行结果:

var res = Demo3.EXTENT_BOTTOM_UP_CUT_ROD(Demo1.p, 10);
var r = res.Item1;
var s = res.Item2;
Console.Write("i\t");
for (var i = 0; i < r.Length; i++) Console.Write("{0}\t", i);
Console.WriteLine();
Console.Write("r[i]\t");
for (var i = 0; i < r.Length; i++) Console.Write("{0}\t", r[i]);
Console.WriteLine();
Console.Write("s[i]\t");
for (var i = 0; i < r.Length; i++) Console.Write("{0}\t", s[i]);

Console.Write("方案\t");
for (var i = 0; i < r.Length; i++) {
  if (i == s[i]) {
    Console.Write("不切\t");
  } else {
    Console.Write("{0}+{1}\t", i - s[i], s[i]);
  }
}

说明

这个算法还是存在一定缺陷, 例如在 $n = 7$ 的时候有两种方案, 这例只会给出两个方案, 即只切成两段的方案.